تحديد إحداثيات مركز ثقل مساحات السطوح -  الجزء الأول

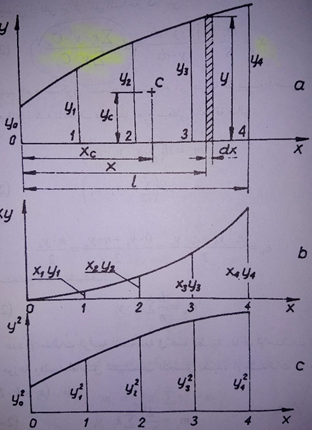
بفرض وجود خط منحنٍ مبين في الشكل التالي، تحدد إحداثيات مركز ثقل مساحة السطح أسفل هذا المنحني بتقسيم العزم السكوني لهذه المساحة بالنسبة إلى المحور المختار على قيمة هذه المساحة، لتحديد الإحداثي الأفقي لمركز ثقل المساحة x_c ينبغي حساب العزم السكوني لهذه المساحة بالنسبة إلى المحور y (أو بالنسبة لأي محور موازٍ لهذا المحور)، بفرض أن المساحة العنصرية تساوي dS=y.dx فإن العزم السكوني العنصري لهذه المساحة سيساوي  ،  العزم السكوني لكامل المساحة يساوي:

إذا لم يكن الخط المنحني معرف بمعادلة رياضية لكن معطى تخطيطياً أو بيانياً عندئذ يمكن قياس الإحداثيات الرأسية عند نقاط اختيارية وبالتالي فإن التكامل الأخير يمكن حسابه رقمياً، عند استخدام قاعدة سيمبسون I فإن العزم السكوني m_y سيعطى بالعلاقة التالية:

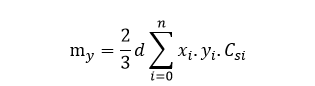
تمثل قيمة هذا العزم المساحة أسفل المنحني المبين في الشكل التالي حيث إن كل إحداثي رأسي يمثل حاصل جداء الإحداثي y_i ببعده x_i عن المحور المختار.

يفضل عند إجراء حسابات الاتزان الخاصة بالسفن استخدام الإحداثي الأفقي x_i بصورة لا بعدية r_i=x_i/d نظراً لكبر بدن السفينة حيث إن d يمثل كما نعلم طول قطاع التقسيم أي المسافة الفاصلة بين إحداثيين رأسيي متتاليين ومنه:

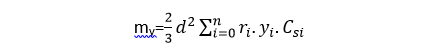
يحدد الإحداثي الأفقي لمركز ثقل المساحة كما يلي: