العلاقة بين عزوم العطالة بالنسبة إلى محاور متوازية

العلاقة بين عزوم العطالة بالنسبة إلى محاور متوازية

& إن عزم العطالة للشكل المركب، يساوي مجموع عزوم العطالة لأجزائه المفردة.

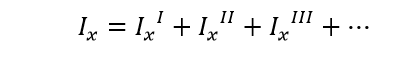
وهذا يستنتج مباشرة من خصائص التكامل المحدود:

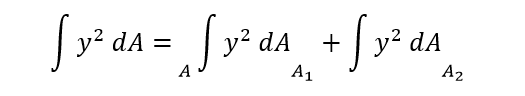
حيث :    

وعلى هذا الأساس فلحساب عزم العطالة للشكل المركب، يجب تقسيمه إلى عدة أشكال بسيطة، وبحساب عزوم العطالة لهذه الأشكال وجمعها نحصل على العزم المطلوب.

إن النظرية المذكورة تنطبق أيضا بالنسبة لجداء العطالة أو عزم العطالة الطارد المركزي.&

& ولإيجاد العلاقة بين عزوم العطالة بالنسبة إلى محاور متوازية نفرض مايلي:

ليكن لدينا المقطع المبين بالشكل والمطلوب تعيين عزوم العطالة وجداء العطالة بالنسبة لمحور ما  ، الشكل رقم (1).

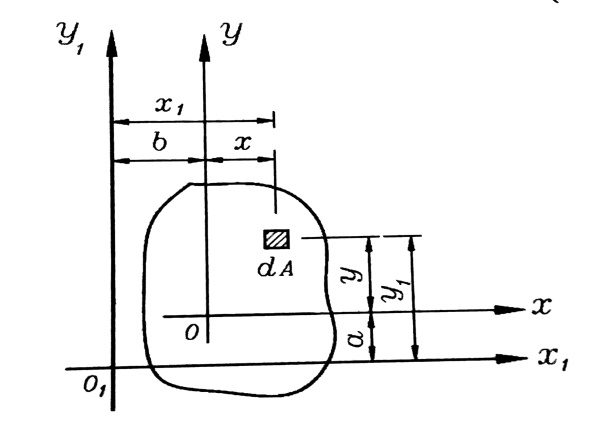
 الشكل رقم (1)

نفترض أن :  هو المحور المركزي، وأن عزم العطالة  معلوم.

من الشكل رقم (1)، نجد أن:        إذن :

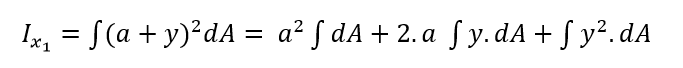
إن التكامل الأول يعطينا مساحة المقطع، والتكامل الثاني يمثل العزم الستاتيكي بالنسبة للمحور المركزي  ، ويساوي الصفر.

أما التكامل الثالث فيمثل عزم العطالة   لمقطع بالنسبة للمحور  ، وعلى هذا الأساس فإن:

أي أن عزمالعطالة بالنسبة لأي محور يساوي عزم العطالة بالنسبة للمحور المركزي الموازي له، مضافا له حاصل ضرب مساحة المقطع أو الشكل بمربع البعد بين المحورين.

ويتضح من العلاقة السابقة، أن عزم العطالة بالنسبة للمحور المركزي أقل من عزم العطالة بالنسبة لأي محور غير مركزي مواز للأول.

إن عزم العطالة بالنسبة لمحور مركزي يسمى بعزم العطالة المركزي.