تعطي هذه الطريقة نتائج أكثر دقة بالمقارنة مع طريقة شبه المنحرف، تعتمد هذه الطريقة على استبدال كل قطاع من المنحني المدروس محدد بثلاثة إحداثيات رأسية متجاورة تفصلهم مسافات متساوية، بتابع منحني من الدرجة الثانية معادلته:
Y=a.x2+b.x+c
لاستخراج معادلة سيمبسون I نأخذ قطاعاً من منحنٍ وهو ABC محدد بثلاثة احداثيات رأسية متوضعة على مسافات متساويةd من بعضها، تحسب مساحة السطح المحدد بالنقاط x0,A,B,C,x2,x0 تقريباً كما يلي:
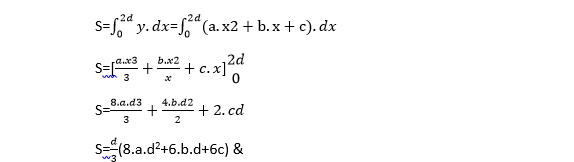
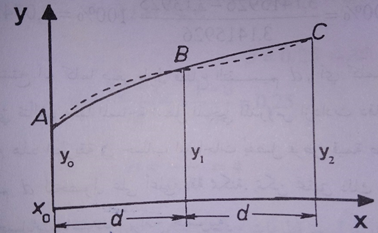
تحدد قيم الاحداثيات الرأسية بعد تعويض قيم الاحداثيات الأفقية المقابلة لها في معادلة التابع من الدرجة الثانية:

وعادة معادلة سيمبسون لقطاع واحد بطول (أو قطاعين طول كل منهما) تأخذ شكل:
إذا كان مجال منحني التابع كبير أو إذا أردنا الحصول على نتائج أكثر دقة عندئذ تجزأ قاعدة المنحني إلى عدد زوجي من الأجزاء أو القطاعات ذات الأطوال المتساوية، تحدد المساحة الكلية بجمع المساحات الجزيئة المحددة مع العلم أن كل مساحة جزئية محصورة بين ثلاثة إحداثيات رأسية متتالية بطول كما في الشكل التالي









