الإجهادات الرئيسية وثوابت الحالة الإجهادية
ليكن لدينا الشكل رقم (1) و بالعودة للعلاقات رقم (4) من مقال الحالة الإجهادية الحجمية وبفرض أن المقطع المائل BCD هو ساحة رئيسية ، عندئذ الإجهاد الكلي في هذا المقطع سيتجه وفق الناظم v والذي رمزنا له بالرمز S ، وبالتالي يكون :
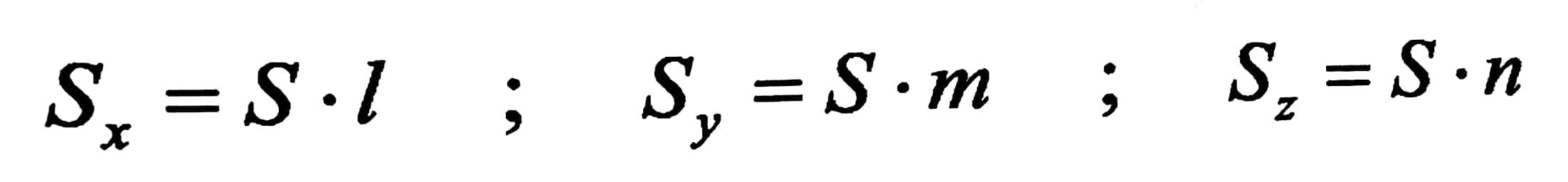
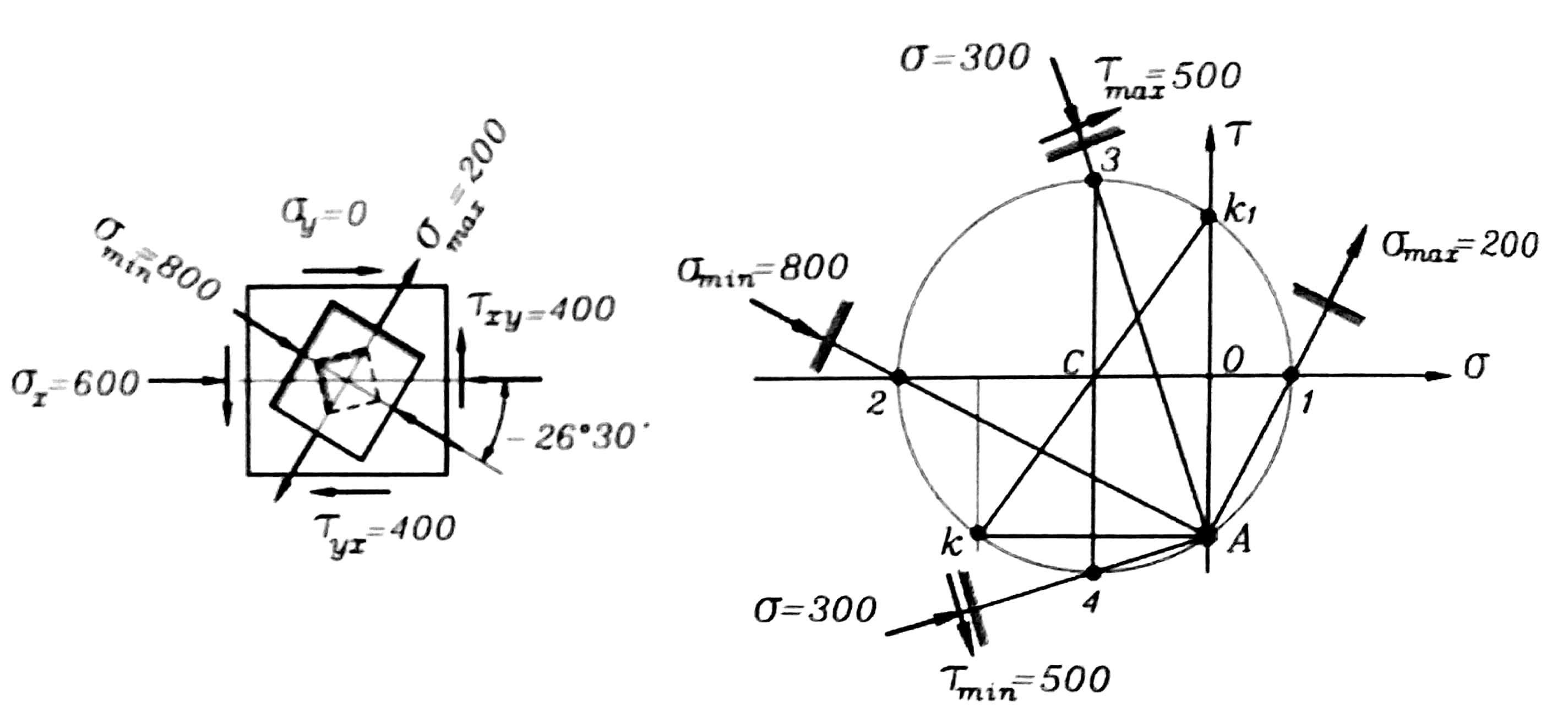
الشكل رقم (1)
وستأخذ العلاقات :
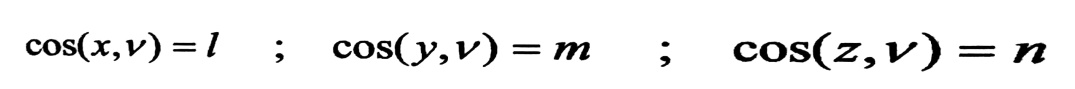
الشكل التالي :
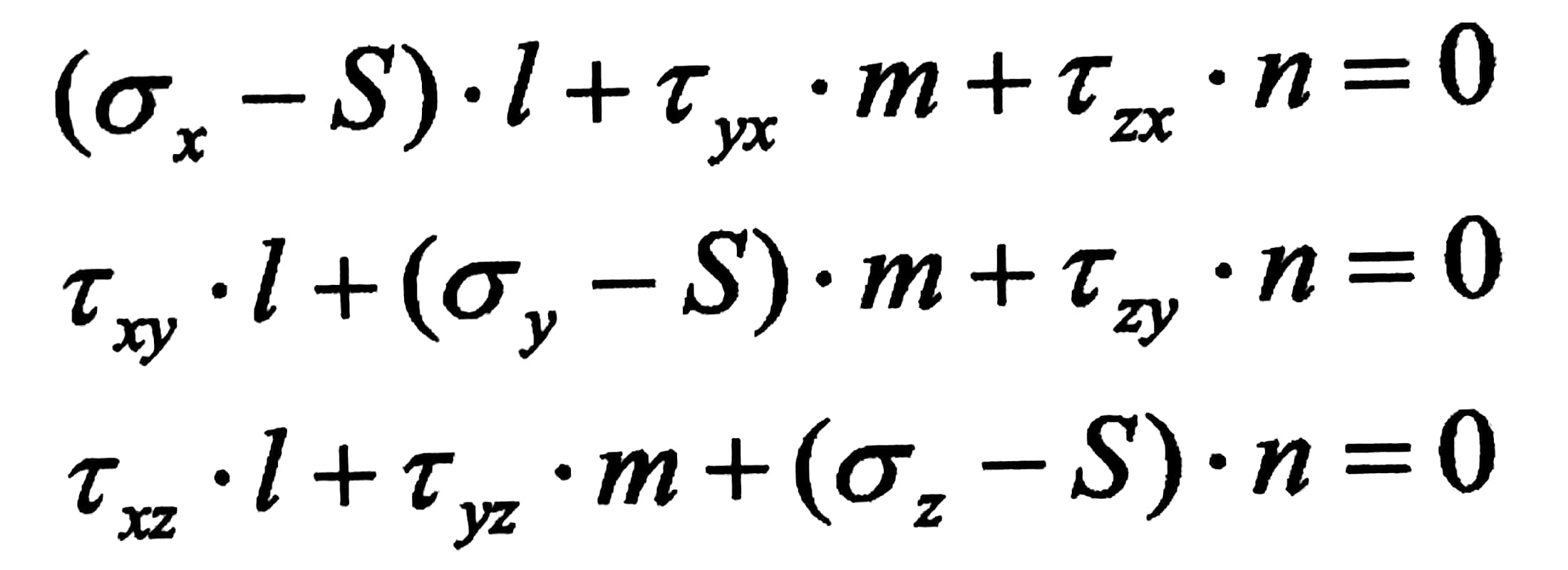(1)
يمكننا أن ندرس هذه العلاقات كمجموعة معادلات خطية بالنسبة للمجاهيل (1 , m , n) ، التي تعين اتجاه المقطع " الساحة " الرئيسي في مجموعة الإحداثيات x,y,z .
وبما أن التجيبات الموجهة لا يمكن أن تكون جميعها وبنفس الوقت مساوية للصفر ، إذ أن :
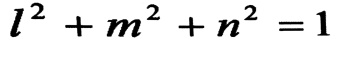(2)
وبالتالي فإنه حتى يكون هناك حلا للمعادلات الثلاث رقم (1) ، مختلفا عن الصفر يجب أن يكون معين الأمثال يساوي الصفر .
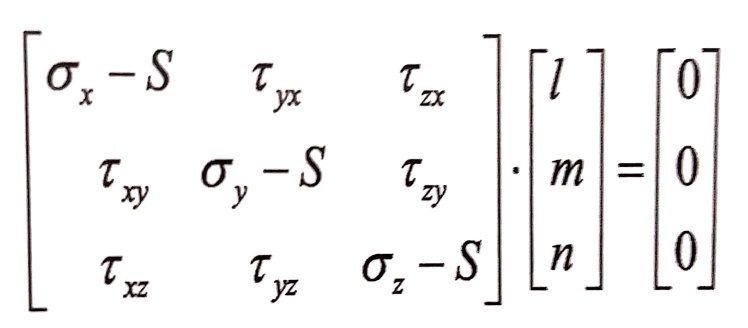
بحل هذا المعين وترتيب حدوده وفق درجة S نحصل على المعادلة التكعيبية التالية :
قم بتنزيل تطبيق eMufeed Android الآن
