فتل القضبان الرقيقة الجدران
تلقى القضبان رقيقة الجدران استخداما واسعا في أغلب مجالات الإنشاءات الهندسية وكثيرا ما تظهر ضرورة حساب مثل هذه العناصر على الفتل .
ومن أهم المميزات الهندسية لهذه المقاطع هو أن سماكتها أصغر بكثير من بقية أبعادها . بدقة كافية يمكن اعتبار توزع الإجهادات على سماكة المقطع العرضي خطية وموزعة بصورة منتظمة .
تختلف طريقة حساب مثل هذه العناصر على الفتل حسب ما تكون مقاطعها العرضية مغلقة أو مفتوحة .
القضبان ذات المقاطع المفتوحة :
من أجل تعيين الإجهادات والتشوهات لقضيب رقيق الجدران ذي مقطع عرضي مفتوح ومعرض للفتل ، الشكل رقم (1) ، يمكن اعتبار الإجهادات في المقطع الرقيق المفتوح هي نفسها فيما لو فتح هذا المقطع وأخذ شكل مستطيل . وبالتالي يمكن استخدام العلاقات المذكورة في مقال الطاقة الكامنة عند الفتل من أجل القضبان ذات المقطع المستطيل .
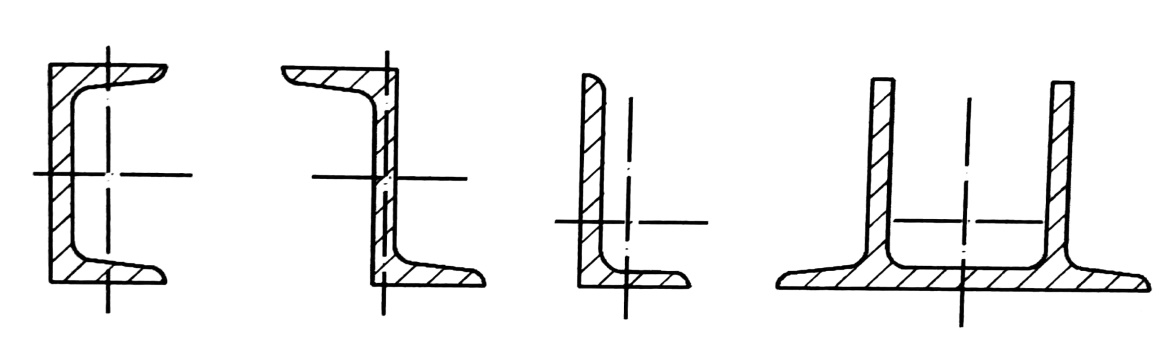
الشكل رقم (1)
لذلك يقسم المقطع إلى مجموعة مستطيلات عرضها أصغر بكثير من طولها . ومن الجدول يتضح أنه للمقاطع المستطيلة الضيقة التي تكون نسبة أضلاعها a/b ≥ 10 تكون العوامل α و β تساوي α = β ≈ 1/3
|
نوع المقطع |
قيمة المعامل η |
|
مقطع زاوي L |
100 |
|
مقطع شكل I |
120 |
|
مقطع شكل T |
115 |
|
مقطع شكل مجرى |
112 |
ويمكن تعيين الخواص الهندسية It لتلك المقاطع المفتوحة التي تتكون من مستطيلات رفيعة طويلة
(a/b ≥ 10) من العلاقة :
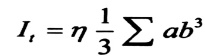
حيث :
η : معامل يعتمد على شكل المقطع .
a : طول الضلع الكبير (الطويل) للمستطيل .
b : طول الضلع الصغير (السماكة) للمستطيل .
والإجهادات المماسية العظمى توجد في المستطيل الذي له أكبر عرض (سماكة) ، وتحدد بالعلاقة :
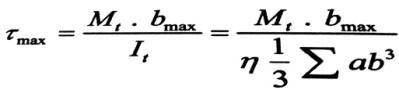 (1)
(1)
وذلك لأن :
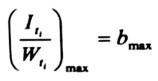
حيث :
Bmax : أكبر قيمة لضلع المستطيل القصير .
وتحدد زاوية الفتل بالعلاقة التالية :
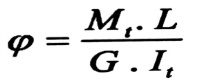 (2)
(2)
وللمقاطع المدلفنة المفتوحة والرقيقة الجدران ، تعطى قيمة It في جداول خاصة . كما أن قيمة It لمثل هذه المقاطع (الرقيقة الجدران وذات المقطع المفتوح) قليل جدا بمقارنته مع قيمة It للقضبان ذات المقطع الدائري الأصم ، الذي له نفس المساحة . لذلك من الأفضل عدم استعمال مثل هذه القضبان عند تعرضها للفتل .
في الفتل غير الحر أو ما يسمى بالمقيد حيث يصعب اعوجاج المقاطع العرضية ، فإن العلاقات المذكورة أعلاه غير صالحة للاستعمال .
- إن النظرية العامة للفتل المقيد للقضبان الرقيقة الجدران ذات المقطع المفتوح ، درست بشكل واسع من قبل العالم الروسي فلاسوف الذي أوجد أنه في حالة الفتل المقيد تظهر في المقاطع العرضية إجهادات كبيرة ناظمية ومماسية إضافة إلى الإجهادات المماسية الناتجة عن الفتل الصافي والتي حسبت في العلاقات السابقة أعلاه .
القضبان ذات المقطع المغلق :
تعتبر القضبان الرقيقة الجدران ذات المقطع المغلق أكثر صلابة ، ولذلك فهي أكثر ملاءمة للاستعمال على الفتل أو الالتواء .
لنأخذ القضيب الأسطواني المبين مقطعه العرضي في الشكل رقم (2) .نفترض أن سماكة الجدار t تتغير بسلاسة حول محيط المحيط ولذلك يمكن إهمال تركيز الإجهادات .
ونظرا لقلة سماكة الجدار ، فيمكن اعتبار الإجهادات المماسية ꚍ التي تظهر عند الفتل موزعة بصورة منتظمة على السماكة .
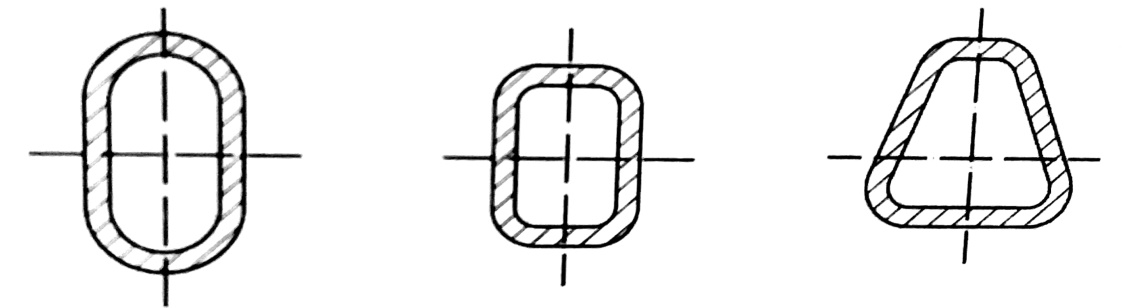
الشكل رقم (2)
ومن المفاهيم الضرورية عند فتل القضبان الرقيقة الجدران ذات المقطع المغلق ما يلي :
-1 المحل الهندسي للنقاط المتساوية البعد عن المحيط الداخلي والخارجي للمقطع العرضي تدعى بالخط المتوسط للمقطع .
-2 وبالتالي من أجل تلك القضبان ذات السماكات الصغيرة يمكن أن نقبل الفرضية التالية :
(( إن الإجهادات المماسية الناتجة عن عزم الفتل ستكون موزعة بشكل شبه منتظم على سماكة القضيب ومتجهة بشكل مماسي للخط المتوسط )) .
-3 ومن الضروري ذكر الفرضية :
(( إن حاصل جداء ꚍ.t على كامل محيط المقطع هو مقدار ثابت : ꚍ.t = const . أي حيث يكون المقطع أضيق يكون الإجهاد أكثر والعكس صحيح )).
لنوجد الآن العلاقة التي تربط بين عزم الفتل وقيمة الإجهادات المماسية التي تظهر في المقطع العرضي للقضيب . ولأجل هذا يتم البحث في توازن القسم المقطوع من القضيب المبين مقطعه العرضي في الشكل رقم (3) .
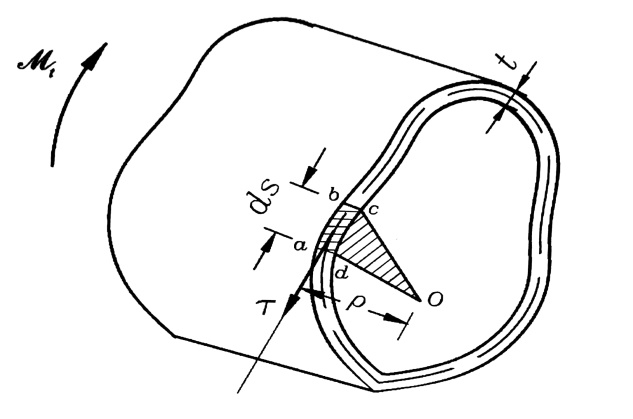
الشكل رقم (3)
إن القوة التي تؤثر على المساحة الأولية أو العنصرية t.ds تساوي ꚍ.t.ds ، أما عزم الفتل الذي تسببه هذه القوة الأولية بالنسبة لنقطة اختيارية o تقع في مستوي المقطع العرضي ، فإنه يساوي إلى : p .ꚍ.t.ds .
حيث :
p : ذراع تأثير القوة بالنسبة إلى النقطة .
ولكي يتوازن قسم القضيب المقطوع ، فإنه من الضروري أن يكون مجموع العزوم بالنسبة للمحور المار بالنقطة oوالموازي لمولد أو راسم سطح القضيب مساويا للصفر :
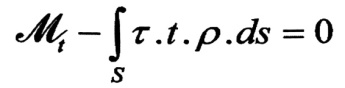
حيث يمتد التكامل على طول المحيط s كله ، ولكن حاصل p .ds يساوي ضعف مساحة المثلث oab :
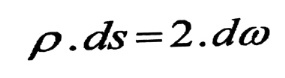
إذن :
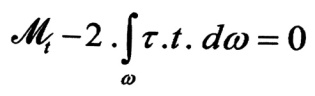
وبما أن حاصل الضرب ꚍ.t = const هو مقدار ثابت ، لذلك يمكن نقله خارج إشارة التكامل .
ويبقى المقدار 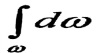 تحت إشارة التكامل فقط ، و
تحت إشارة التكامل فقط ، و









