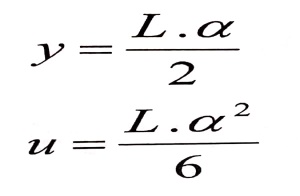تعيين الإزاحات في الجوائز المعرضة للانعطاف
للحكم على مدى صلاحية عمل جائز معرض للانعطاف ، لا تكفي معرفة قيمة الإجهادات التي تظهر في مقاطعه نتيجة تأثير الحمولة المعطاة إذ أن حساب الإجهادات يسمح لنا بالتحقق من متانة المنشأ ، لكن الجائز المحقق على المتانة يمكن أن يظهر غير صالح للاستثمار بسبب ضعف صلابته ، فإن كان الجائز ينحني بشكل كبير تحت تأثير الحمولة فعند استثمار المنشأ تظهر مشاكل وصعوبات كبيرة ، ولحساب صلابة الجائز لا بد من تحديد الانتقالات لنقاط مختلفة من محوره .
لدراسة الجوائز ذات المقاطع العرضية التي تملك محور تناظر ، والتي تؤثر عليها حمولات خارجية واقعة في المستوى المنطبق مع محاورها . نأخذ الشكل رقم (1-a) الذي يبين جائزا انحنى محوره تحت تأثير قوة مركزة في طرفه ، إن النقطة k الواقعة على المحور ، وفي مقطع يبعد x من مبدأ الإحداثيات ، ننتقل إلى k` .
نرمز لانتقال نقطة ما من محور الجائز بالاتجاه y بالرمز y ، وللانتقال باتجاه محور الجائز x بالرمز u ، وإذا أخذنا في النقطة k` مماسا لمحور الجائز المنحني فسيشكل مع محور الجائز قبل الانحناء زاوية مقدارها ϕ هي مركبات الانتقالات للمقطع العرضي الاختياري للجائز .
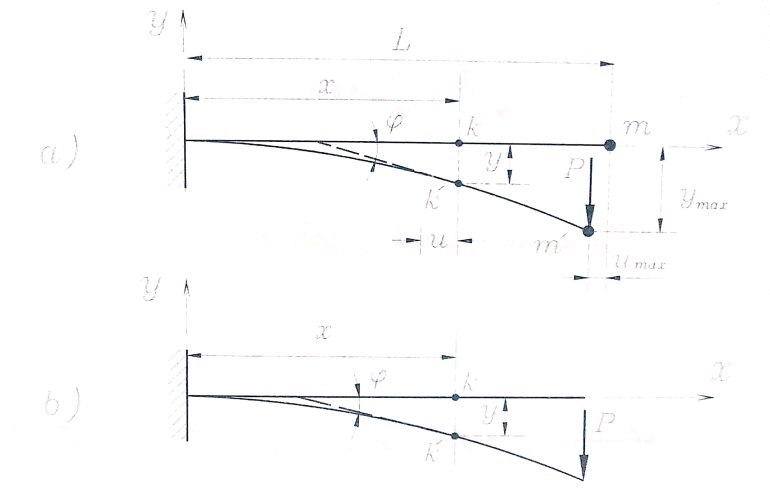
الشكل رقم (1)
وانطلاقا من اعتبارات علمية ، تحدد قيمة السهم الأعظمي المسموح به ، للجائز بالعلاقة :
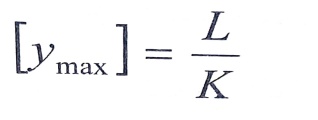
حيث :
L : طول مجاز الجائز .
K : مقدار عددي تحدده الكودات التصميمية ، وهو بحدود (300→1000) ، ويعتمد على الغرض الذي أقيمت من أجله القطعة أو الآلة ، مثلا من أجل منشأة هامة كجسر سكة حديدية إن قيمة K حوالي (1000).
ومن هنا نرى أن للسهم عند الانعطاف قيمة صغيرة مقارنة بمجاز الجائز ، وهذا يسمح بقبول عدة فرضيات :
الفرضية الأولى :
عند السهوم الصغيرة ، يمكن تحديد زاوية ميل المماس لمحور الجائز المنحني بالعلاقة :
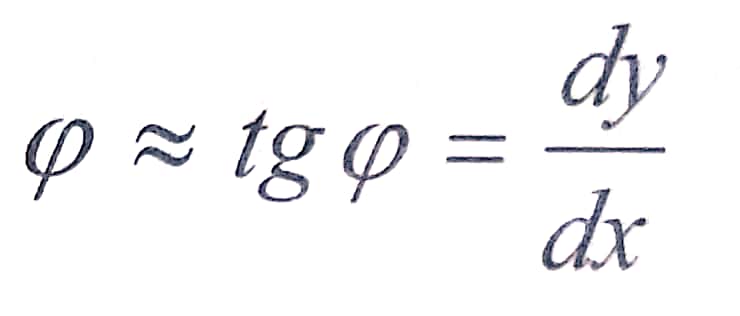
الفرضية الثانية :
يمكن إهمال الانتقالات الأفقية u ، حيث أنها ذات قيمة صغيرة مقارنة بقيمة y .
فلو أخذنا جائز طوله L موثوقا من طرف ، الشكل رقم (2) ، وفرضنا أنه قد انحنى بشكل دائري فإن الانتقالين الشاقولي والأفقي للنهاية الحرة يساويان :
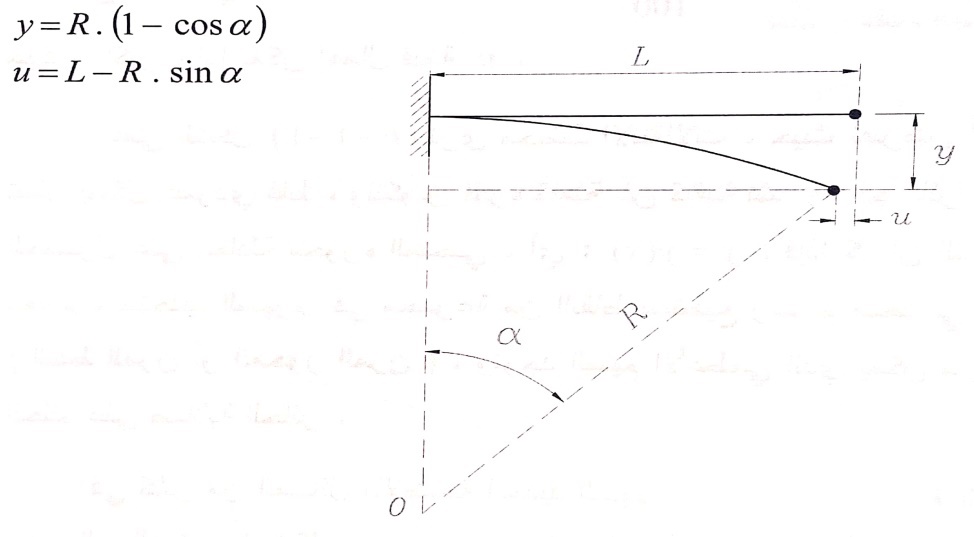
الشكل رقم (2)
حيث :
R = L/α : نصف قطر التقوس .
α : زاوية دوران المقطع العرضي الطرفي .
لننشر cos α و sin α في سلسلة ولنكتفي بحدين من كل منهما بسبب صغر α .
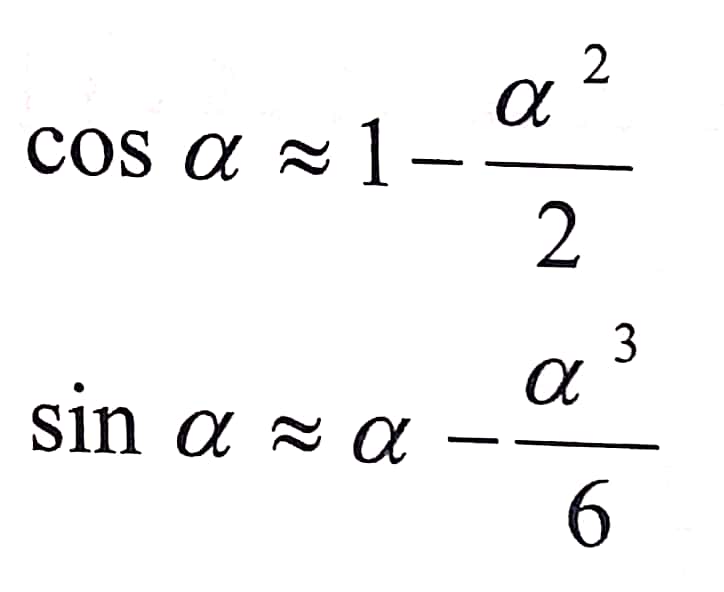
بالتعويض نجد :