تركيز الإجهادات
عند التغير المفاجئ لمحيط المقطع العرضي أو الطولي للعمود يظهر تركيز في الإجهادات . ويحسب تأثير الإجهادات بواسطة معامل التركيز الذي يحدد إما نظريا بطرق نظرية المرونة وإما عن طريق التجارب .
وقد أعطي في الشكل رقم (1) رسم بياني لتحديد مقدار المعامل النظري لتركيز الإجهادات tα عند فتل قضيب مؤلف من جزأين يتصلان مع بعضهما البعض بمنحني اتصال نصف قطره p .
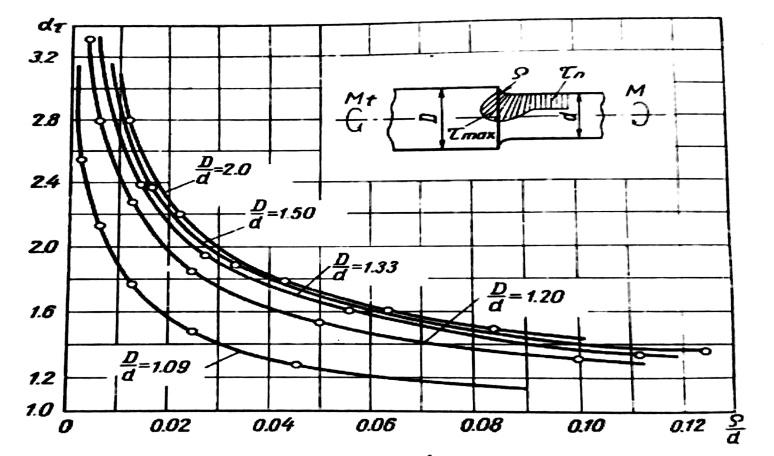
الشكل رقم (1)
كما أنه عند الانتقالات المفاجئة ، أي عندما تكون قيم p/d صغيرة ، فإن tα تزداد بشكل كبير .
وعندما يكون معامل تركيز الإجهادات معلوما ، فإن الإجهاد المماسي الأكبر للمقطع العرضي الدائري يحدد حسب العلاقة :
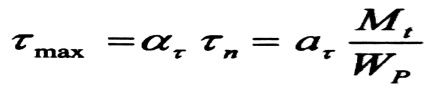
حيث :
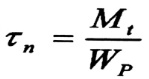
الإجهاد الاسمي المحسوب بالنسبة لأصغر مقطع عرضي .
- إن الحالات التي يؤخذ فيها تأثير تركيز الإجهادات في الاعتبار ، هي :
أ- عند تأثير الأحمال الستاتيكية بالنسبة للمواد المنخفضة اللدونة وللمواد القابلة للتحطم الهش .
ب- عند تأثير الأحمال المتغيرة (دراسة التعب) بالنسبة لجميع المواد .
ولأجل التقليل من تأثير تركيز الإجهادت ، يجب الابتعاد عن التغيرات المفاجئة في محيط المقطع ، وذلك باستعمال منحنيات انتقالية بأكبر نصف قطر ممكن .
الأشكال المنطقية للمقاطع التي تعمل على الفتل :
إن الأفضل بين مقطعين لهما عزم مقاوم قطبي Wp أو Wt متساو ، ولهما نفس عزوم الفتل المسموح بها ، هو ذلك المقطع الأقل مساحة ، أي الذي يضمن أقل استهلاك للمواد ، وبما أن النسبة (Wp/A) أو (Wt/A) تعتبر كمية بعدية فلأجل مقارنة المقاطع المختلفة يكون من السهل استعمال أحد المقادير غير البعدية :
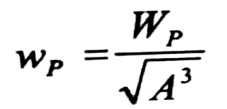
أو في المقطع غير الدائري يكون :
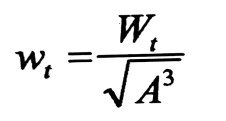
حيث :
Wp و Wt تسمى العزم المقاوم النوعي على الفتل " وحدة العزم المقاوم عند الفتل " .
وتوجد في الجدول رقم (1) قيم للمقدار Wt موافقة لبعض المقاطع العرضية .
الجدول رقم (1) : العزم المقاوم النوعي على فتل لمقاطع مختلفة :
|
نوع مقطع القضيب |
Wt |
|
على شكل مجرى |
0.04 ‒ 0.05 |
|
مقطع على شكل I |
0.05 – 0.07 |
|
مقطع مستطيل عند a/b=10 |
0.1 |
|
مقطع مستطيل عند a/b =2 |
0.18 |
|
مقطع دائري |
0.21 |
|
مقطع دائري أصم |
0.28 |
|
مقطع دائري حلقي C=d/D =0.5 |
0.37 |
|
مقطع دائري حلقي C =d/D = 0.9 |
0.16 |
وكما يتضح فإن
Download eMufeed Android Application Now
