تعيين الإجهادات الناظمية  في حالة الانعطاف الصافي

 تعيين الإجهادات الناظمية في حالة الانعطاف الصافي

لتعيين الإجهادات الناظمية في حالة انعطاف صاف ندرس الجائز المحمل بالحمولات المبينة في الشكل رقم (1) ، حيث يظهر من مخططي عزوم الانعطاف وقوى القص بأن هناك جزء من الجائز تظهر في مقاطعه فقط عزوم انعطاف ثابتة على كامل طوله ، بينما قوى القص تتغيب فيه ، عندئذ نقول بأن هذا الجزء من الجائز يتعرض لحالة الانعطاف الصافي .

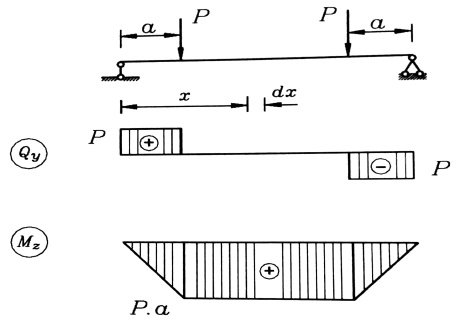
الشكل رقم (1)

ويمكن أن يظهر الانعطاف الصافي ، أيضا ، في حالات مختلفة للحمولات الخارجية نعرض منها حالة القضيب المعرض لعزمي انعطاف والمبين في الشكل رقم (2) ، حيث يتقوس الجائز تحت تأثير هذه الحمولات وتتعرض أليافه العلوية إلى التقلص والسفلية للتمدد .

وعند الانتقال من الليف العلوي إلى الليف السفلي نلتقي بمنطقة لا تتعرض أليافها للتقلص أو للتمدد وهذه المنطقة ندعوها بالمنطقة المحايدة . إن خط تقاطع هذه المنطقة المحايدة مع المقطع العرضي يدعى بالمحور المحايد أو بالمحور السليم . أما الوجهين الطرفيين ، وكما هو الحال بالنسبة لكافة المقاطع العرضية للجائز ، فيدوران قليلا بعد أن كانا متوازيين قبل التحميل .

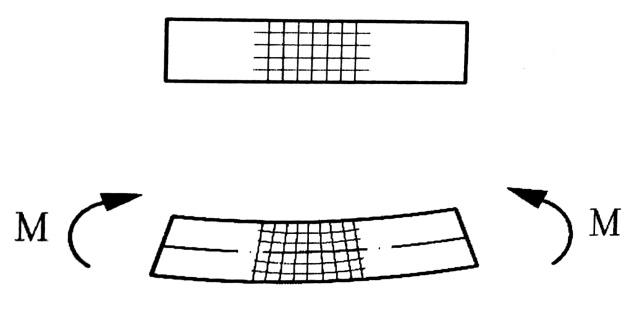
الشكل رقم (2)

- يعتمد في دراسة الإجهادات الناتجة في الجوائز المعرضة للانعطاف من فرضيات نظرية المرونة التي أثبتتها التجارب وهي :

-1 فرضية برنولي : " فرضية المقاطع المستوية " والتي تنص على أن المقاطع العرضية للعنصر تبقى مستوية بعد تشوه العنصر وذلك تحت تأثير الحمولات الخارجية .

-2 الألياف الطولية للجائز لا تضغط على بعضها البعض بعد التشوه .

-3 جميع القوى الخارجية المؤثرة على الجائز تقع في مستو واحد يمر من محور الجائز .

ولوضع قانون لتوزع الإجهادات الناظمية في المقاطع العرضية للجائز وتحديد مقدارها ، فإن معادلات التوازن  لا تكفي ، ومن الضروري استعمال شروط تشوه الجائز الموضح بالشكل رقم (2) ، ومن أجل ذلك نقتطع عنصرا dS من منطقة الانعطاف الصافي ونرسم هذا العنصر بشكل أكثر تفصيلا ، الشكل رقم (3) .

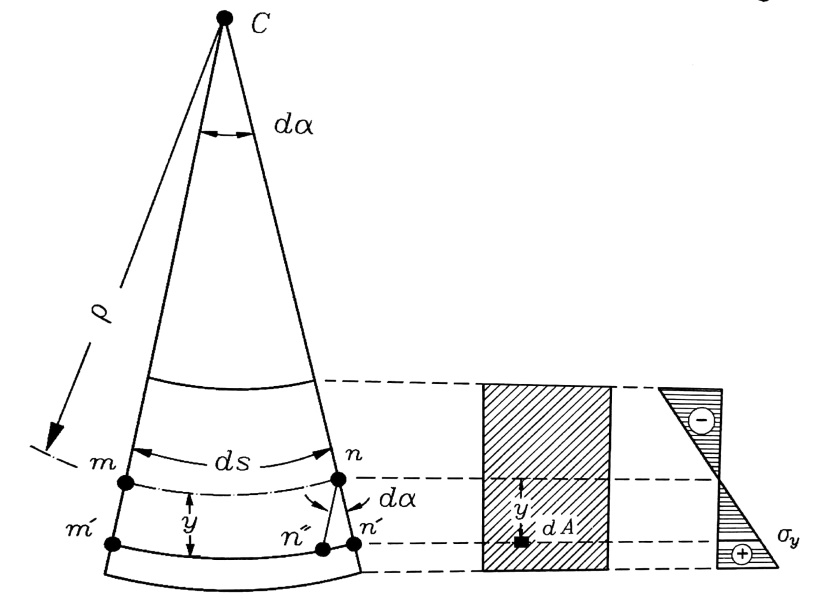
الشكل رقم (3)

لنفرض أن الليف mn واقع في المنطقة المحايدة وبالتالي طوله ثابت لا يتغير ويبقى مساويا لقيمة dS .