الإجهادات المماسية الأعظمية
تبين لنا سابقاً بأنه تمثيل الحالة الإجهادية المستوية في نقطة بواسطة إجهادات ومساحات مختلفة. وبما أن الإجهادات المماسية معدومة على المساحات الرئيسية، فإن أبسط تمثيل للحالة المستوية هو تمثيلها بواسطة الإجهادات الرئيسية والمساحات الرئيسية المؤثرة عليها، الشكل رقم (1).
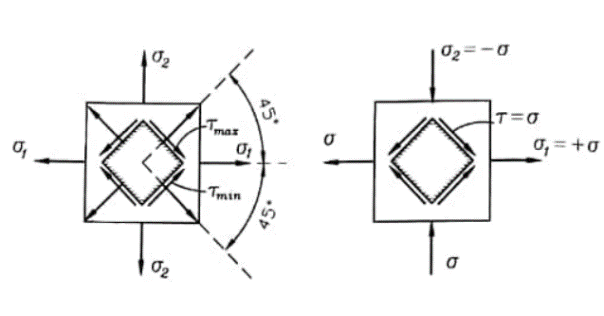
الشكل رقم 1))
وبأخذ الزاوية α اعتباراً من الإجهاد 1σ ، نجد :
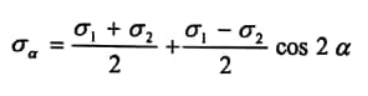...(1)
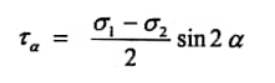...(2)
ولتعيين الإجهادات المماسية rmax. rmin واضح من العلاقة 2 أنه من أجل الزاوية α=+-45ο تكون الإجهادات المماسية حدية (أعظمية وأصغرية) وتساوي:
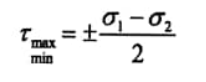...(3)
وبالتعويض من σ1 وσ2 بدلالة σx و σy نجد:
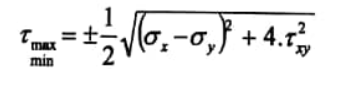...(4)
ولتعيين قيم الإجهادات الناظمية المؤثرة على ساحات الإجهادات المماسية الأعظمية، نعوض الزاوية α=+-45ο في المعادلة 1 الشكل رقم (1) فنجد:
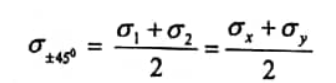...(5)
وفي الحالة المستوية الخاصة، حالة الإجهاد الثنائي المحور المتساوي القيمة والمختلف الإشارة، (إجهاد رئيسي شاد والآخر يساويه ولكنه ضاغط)، أي :
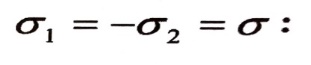...(6)
تكون الإجهادات المماسية الأعظمية :
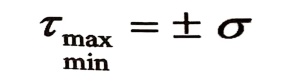...(7)
ومن العلاقة 5 نجد:
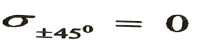...(8)
أي أنه ساحات الإجهادات المماسية تكون الإجهادات الناظمية مساوية للصفر، وتسمى هذه الحالة الإجهادية بحالة القص الصافي.
ويممكننا أيضاً أن نحصل على الإجهادات المماسية الحدية باشتقاق العلاقة بالنسبة لزاوية α ، وبجعل هذا المشتق مساوياً للصفر نحصل على الزاوية التي تعطي قيم الإجهادات المماسية الحدية (عظمى أو صغرى).
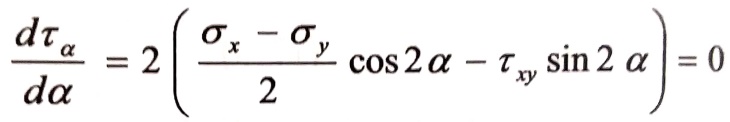...(9)
وتتحقق العلاقة الأخيرة من أجل الزاوية α=β0 التي تحقق العلاقة التالية:
Download eMufeed Android Application Now
