​​​​​​​حساب الإجهادات الناظمية في الساحات الأفقية

 حساب الإجهادات الناظمية في الساحات الأفقية

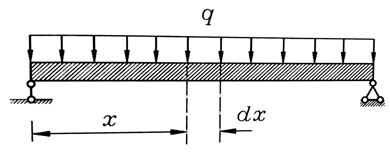
عند استنتاج علاقة الإجهادات الناظمية العلاقة رقم ((3) من مقال تعيين الإجهادات الناظمية في حالة الانعطاف الصافي ) ، كنا قد افترضنا أن الألياف لا تضغط على بعضها البعض وهذه الفرضية صحيحة في حالة الانعطاف الصافي ، ولكن عندما تؤثر على الجائز حمولة موزعة بانتظام بشكل مباشر تظهر إجهادات ناظمية σ_y على الساحات الأفقية ولإيضاح تأثير هذه الإجهادات على متانة الجائز عند الانعطاف ندرس حالة تأثير حمولة موزعة بانتظام كما في الشكل رقم (1) .

الشكل رقم (1)

من أجل ذلك نقتطع من الجائز عنصرا طوله dx الشكل رقم (1) ، فعلى الوجه الأيمن لهذا العنصر تتغير القوى القاصة بمقدار dQ_y .

لنأخذ مقطعا أفقيا على بعد y من المحور المحايد ولندرس توازن الجزء العلوي المقطوع الشكل رقم (2-b) .

من شرط التوازن ∑ Y = 0 ، نجد :

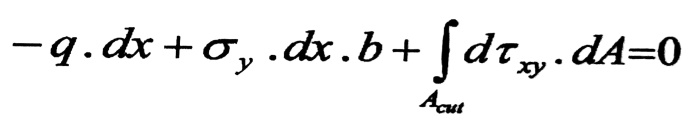
ومن هنا نجد :

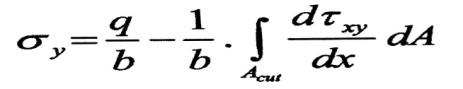   (1)

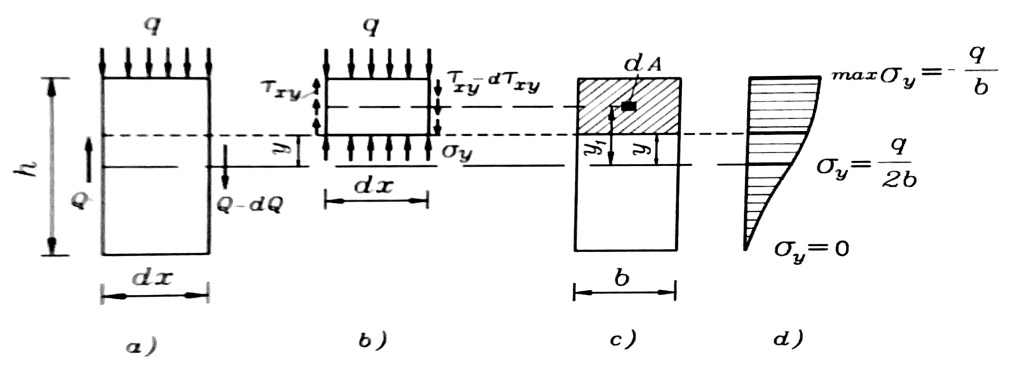
الشكل رقم (2)

وتعطى قيمة الإجهادات المماسية في مساحة تقع على مسافة y₁ من المحور المحايد لمقطع المستطيل بالعلاقة :

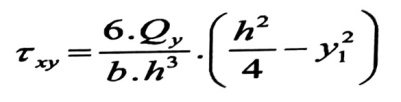
بتفاضل هذه العلاقة بالنسبة لقيمة x ، نجد :

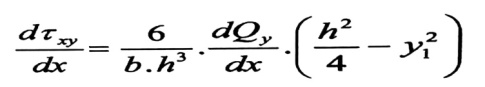   (2)

بتعويض هذه العلاقة في العلاقة رقم (1) ، مع الأخذ بعين الاعتبار أن :

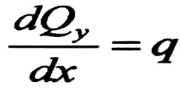
ثم بإجراء التكامل ، نجد :

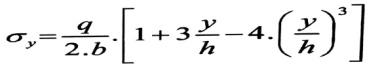
وفي حال :

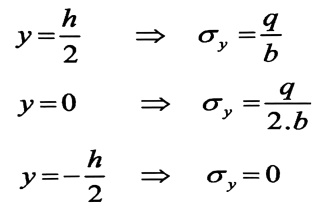
من العلاقة السابقة نجد أن الإجهادات الناظمية الضاغطة σ_y ، تتغير مع ارتفاع المقطع العرضي ، وفق قانون قطع مكافئ من الدرجة الثالثة كما هو واضح بالشكل ونلاحظ أن الإجهادات تكون أعظمية في منطقة تطبيق الحمولة (أي في الألياف العلوية) .

وبشكل عملي فإن قيمة الإجهادات الناظمية σ_y في المقاطع الأفقية يمكن إهمالها أثناء الحساب